Mitigating the risks associated with volcanoes requires a detailed understanding of the transport and eruption of magma through cracks and conduits in Earth's crust. Seismic waves excited by magma flow and its coupling to the elastic wall rocks can be used to place valuable constraints on parts of the volcanic system that are otherwise inaccessible. The complexity of observed seismic signals and the difficulty of modeling the coupled fluid-solid system present a formidable challenge. The objective of this project is to develop numerical models describing the high-speed flow of compressible, viscous fluids through narrow channels in elastic bodies, together with the propagation of seismic waves through the solid. The fluid and solid response is fully coupled: elastic deformation changes the cross-sectional area of the conduit through which fluid flows, and changes in fluid pressure push the conduit walls in and out, exciting seismic waves.
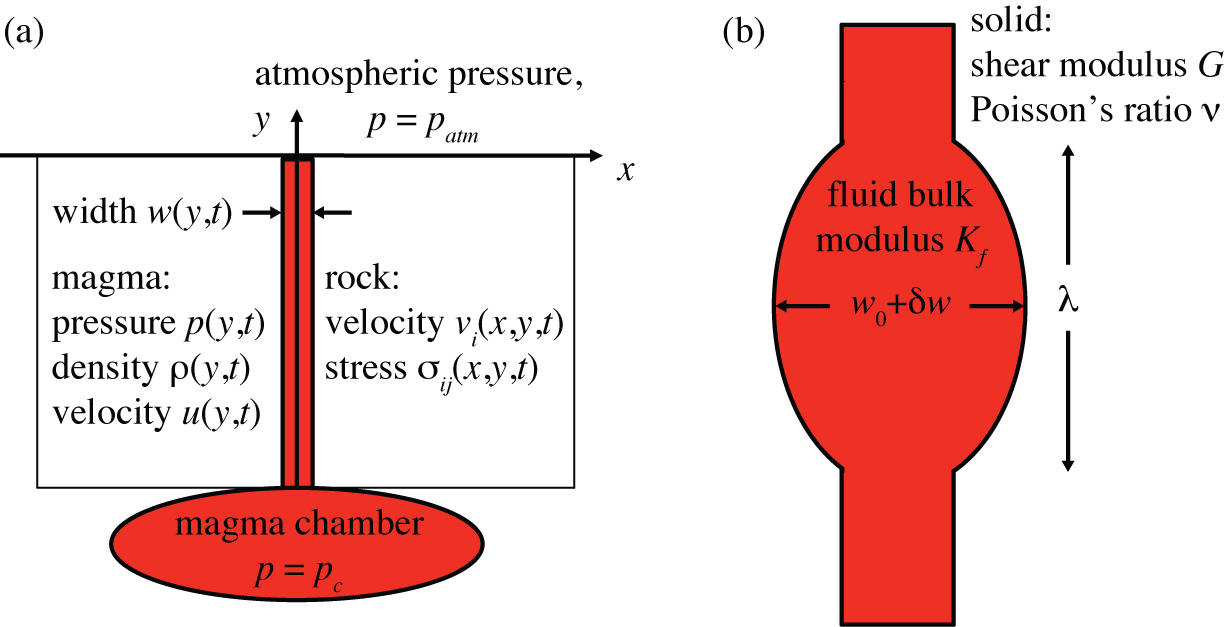
We idealize the volcanic system as shown in Figure 1a. Thus far our models are two-dimensional, with plane strain elastodynamic response. The conduit width is assumed to be smaller than other length scales of interest, permitting us to idealize the conduit as an narrow crack in the solid and to treat the fluid flow using the quasi-one-dimensional approximation. The governing equations express the balance of mass and momentum of the fluid, which is a mixture of liquid melt and exsolved gas. The mass fraction of exsolved gas depends on the pressure through appropriate solubility laws. We include both viscosity and compressibility in our models.
|
|
| Fig. 1: (a) A magma-filled dike cuts through an elastic solid along the plane x = 0. (b) Perturbation to conduit width, used to estimate the importance of wall rock elasticity. |
The fluid and solid are coupled at the conduit walls. The normal tractions on the conduit walls are balanced by the fluid pressure, and the discontinuity in horizontal particle velocity across the conduit equals the rate of conduit opening/closing. An important question to ask is, when is it necessary to consider conduit wall deformation when solving for the fluid flow? The answer depends on the length scale of interest. Consider the response of the system to an instantaneous perturbation of the conduit width, from w0 to w0+δw, over a distance λ, as illustrated in Figure 1b. Deformation of the solid generates internal stresses that act to return to the conduit to its unperturbed width, and compression or expansion of the fluid results in a pressure perturbation. We define the length scale at which these effects balance as the elastic coupling length, λelastic = (πGw0)/((1-ν)Kf). When λ<<λelastic, the solid restoring force is so large that the conduit walls can be effectively regarded as rigid when solving for the fluid flow. In the opposite, long-wavelength limit, the conduit walls become compliant and a complete, two-way fluid-solid coupling is essential. The elastic coupling length, λelastic, can change dramatically with depth and/or magma composition, due to the large variations in fluid bulk modulus, Kf, from gas exsolution.
We have developed and coupled finite difference solvers for fluid flow and seismic wave propagation to solve this problem. The simple example shown in Figure 2 demonstrates our preliminary simulation capabilities. The eruptive fluid is inviscid and obeys a linearized equation of state. Parameters and geometry are similar to those in a basaltic fissure eruption, but without viscosity and changes in compressibility from gas exsolution this model should not be regarded as realistic (this is a new research project!). An initially constant width dike (w0 = 1 m) containing overpressurized magma (Δp = 10 MPa, which balances the initial normal stress σxx in the solid) breaks Earth's surface at t = 0. The general response of the system is characterized by wavelike perturbations propagating along the conduit (Figure 2a). When these perturbations are reflected at the vent and magma chamber, bursts of seismic waves are generated that radiate through the elastic medium (Figure 2b).
|
| Fig. 2: Simulation of a dike containing overpressurized magma intersecting Earth's surface at t = 0 (Click on image to play movie.). (a) Snapshots every 0.5 s of fluid pressure as a function of depth. The drop to atmospheric pressure at the vent at t = 0 drives a rarefaction down into the magma. For a rigid walled conduit (blue), the rarefaction propagates at the fluid sound speed (propagation direction indicated by black arrow). For an elastic walled conduit (red), the fluid-solid coupling leads to dispersive wave propagation, with shortest wavelength modes propagating the fastest. (b) Synthetic seismograms at surface station 200 m from vent (for deformable wall case). Initial P wave is followed by strong Rayleigh wave from initial suction of conduit walls near the vent. Overall trend of velocity indicates downward and inward motion from deflation of the conduit. Diffraction of crack waves from vent at t = 1.5 s creates oscillatory signal. Example shown for inviscid fluid with linearized equation of state. |
The behavior of the system is more complicated when viscous drag is considered. In most cases, the system evolved toward a steady state flow from the high pressure magma chamber to the low pressure atmosphere. The initial wavelike perturbations triggered by the abrupt drop in pressure at the vent at the start of the simulations were damped out. However, for other parameters, the amplitude of the perturbations increased in time. Performing a linear stability analysis revealed that sound waves can be destabilized by the reduction in drag from pressure perturbations that increase the conduit width. It is not yet clear if this instability plays a role in actual eruptions, but it could help explain eruptive tremor.