Supershear Rupture Dynamics

Near-source ground motion is determined by the constructive interference of waves radiated from various parts of the fault. A primary factor determining the character of the ground motion is the speed at which a rupture propagates, an effect known as directivity. Rupture speeds are bounded at the upper end by the maximum speed at which stresses are transmitted through the rock surrounding a fault. See Fig. 1 for more details. While the majority of ruptures have been inferred to have propagated slower than the S-wave speed, several recent strike-slip events appear to have had velocities in excess of the S-wave speed. Supershear propagation of a slip pulse causes radiating shear waves (and Rayleigh waves, for faults near the earth's surface, see Fig. 2) to coalesce into a Mach front. Associated with the Mach front are large velocities and stresses, and geometrical spreading considerations dictate that these large amplitudes will be transported far from the fault.

My work targets many aspects of supershear rupture dynamics. What conditions on the fault give rise to such ruptures? When these conditions are met, what is the exact mechanism that allows the rupture to accelerate to supershear speeds? Is this a phenomenon unique to large earthquakes or does it occur at all scales?

A second focus of my work on supershear earthquakes has been the ground motion produced by these ruptures. How is the ground motion from supershear ruptures different from that produced by subshear ruptures? Is it better or worse in terms of seismic hazard or simply different? What is the appropriate way to incorporate these differences into seismic hazard calculations? I also seek distinguishing features in the near-source velocity and stress fields that can be used to determine the rupture speed and constrain the weakening process of the fault. Using simple rupture models and computational modeling (see Fig. 3), such features were identified in strong motion records of the 2002 Denali Fault earthquake.

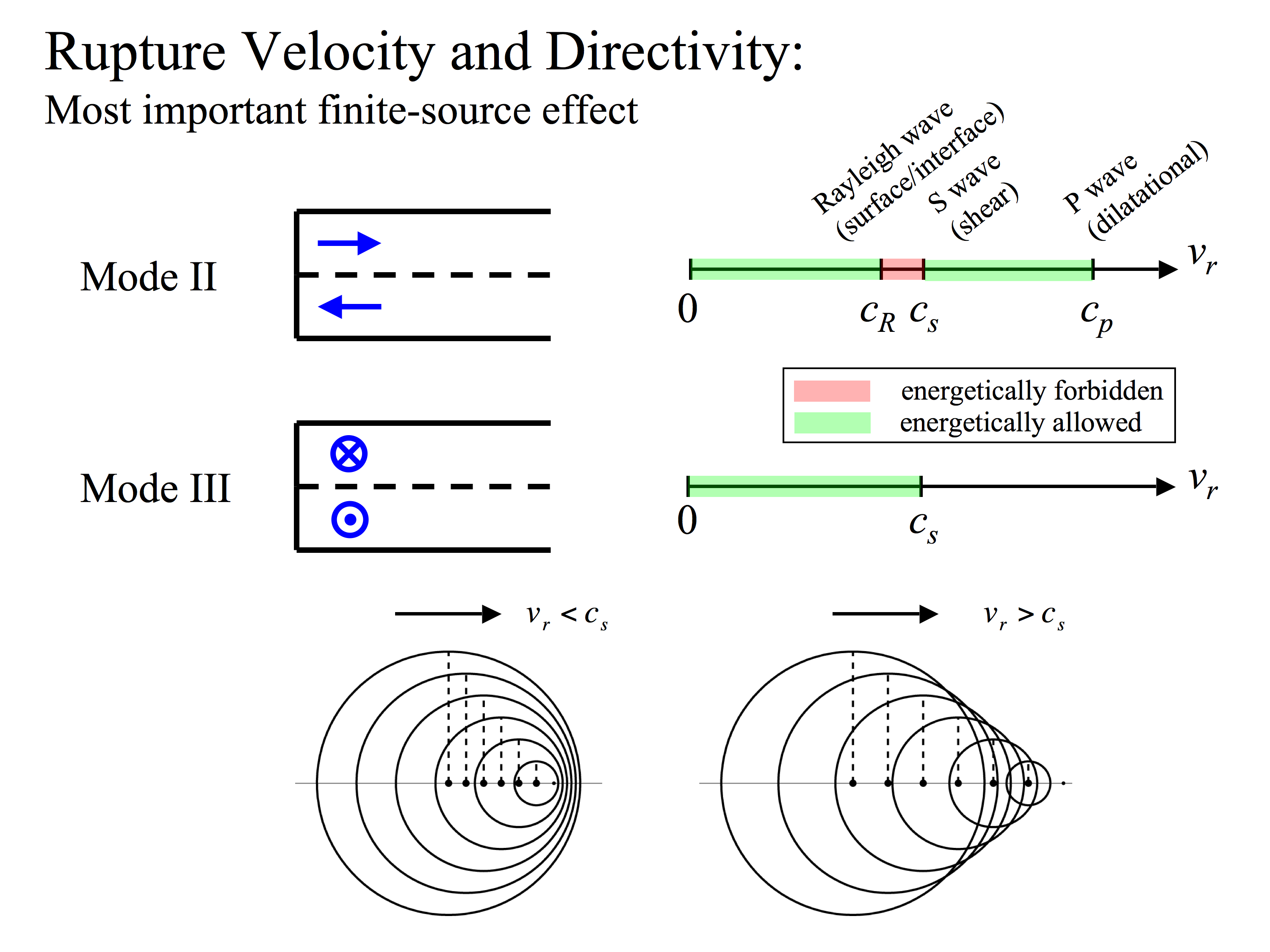
Fig. 1: Permissible values of the rupture speed, vr, are determined by the rupture mode. There are two modes of shear rupture, which are distinguished by the direction of slip relative to the rupture front. In the diagram on the left, the blue arrows indicate the displacement of the two sides of the fault (the fault is the dashed line). Slip in mode III ruptures excites only shear waves, so the S-wave speed, cs, becomes the limiting rupture speed in this geometry. Mode II slip generates both shear and dilational waves, which can interact in rather interesting ways (e.g., to produce Rayleigh surface waves). Mode II ruptures typically propagate below the Rayleigh speed, cR, but can also propagate at intersonic speeds (speeds between the S-wave speed, cs, and the P-wave speed, cp). The difficulty is that ruptures cannot propagate in the narrow speed range between cR and cs (mathematical solutions for such ruptures have the unphysical feature that energy flows out of the rupture front, rather than into it to be dissipated). Understanding how and why ruptures jump between sub-Rayleigh and intersonic speeds is one of my interests.

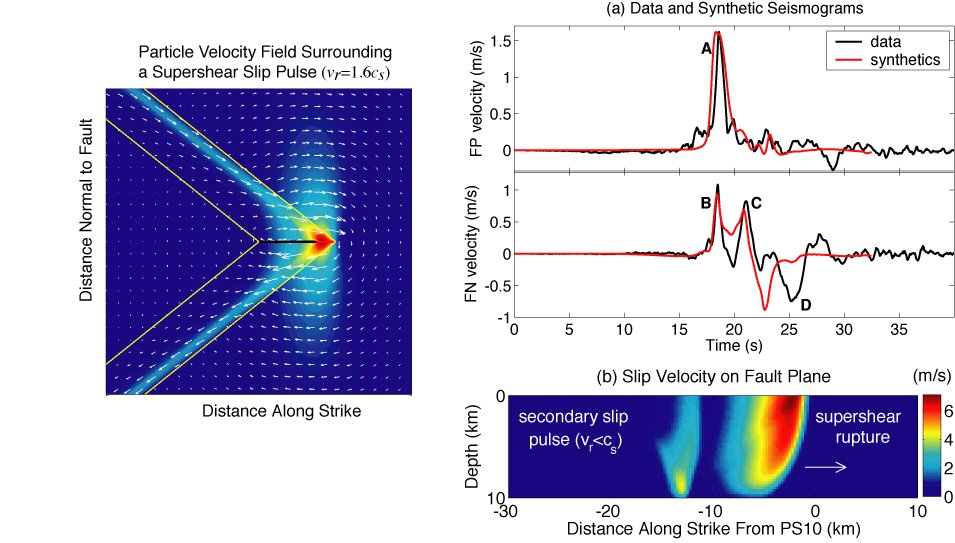
Rupture speed determines how waves from different parts of the fault interfere with each other. At the bottom of the figure are two diagrams illustrating this. They show shear wavefronts emitted when the rupture passes the solid dots. When the rupture is subshear (left), the wavefronts are concentrated in the forward direction and separated in the backward direction. This leads to larger amplitudes and higher frequencies in the forward direction. For supershear ruptures (right), the source outruns the waves and a Mach front is formed.

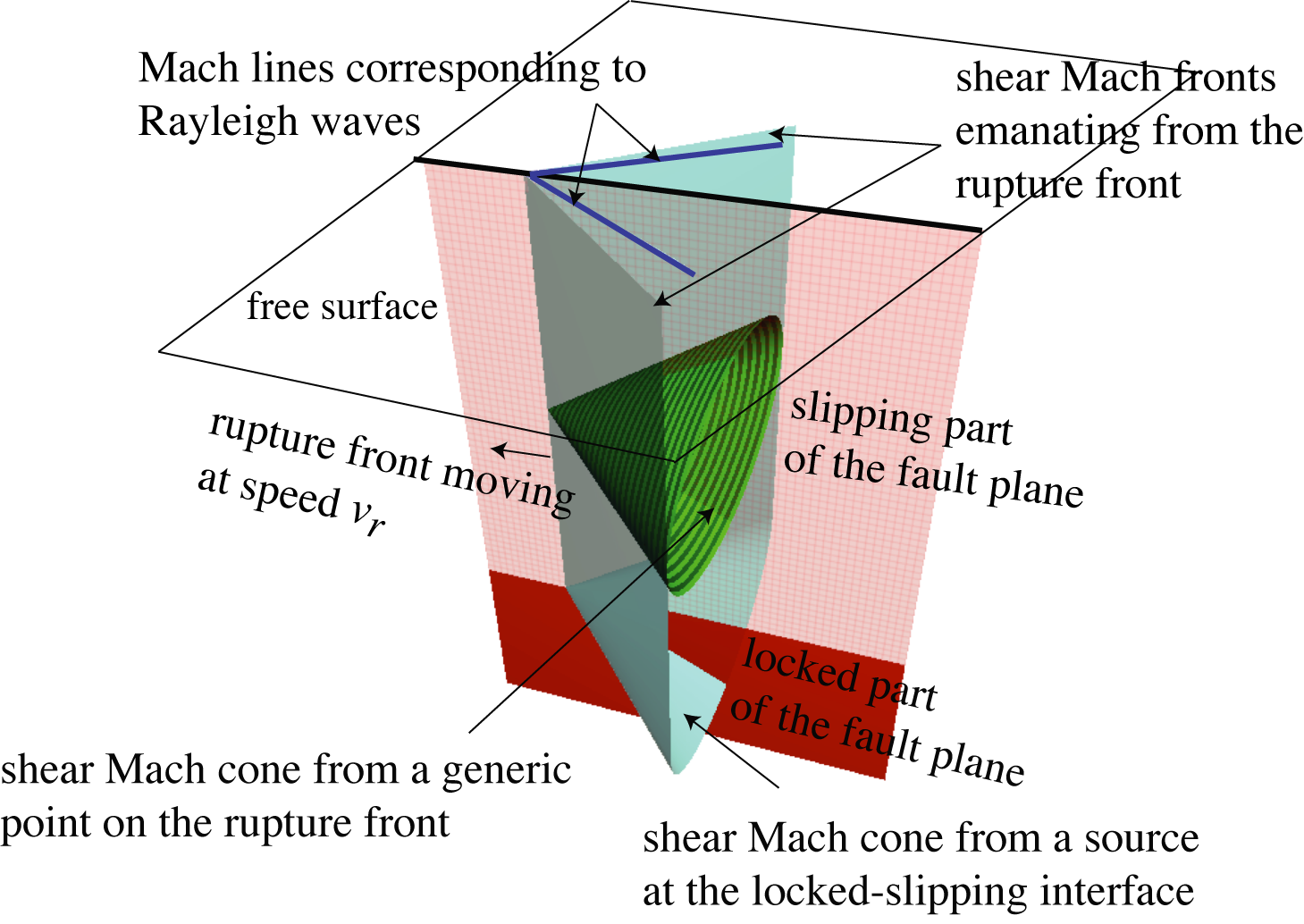Fig. 2: Wavefronts from a three-dimensional supershear rupture on a surface-breaking fault. Each point along the rupture emanates shear waves in the form of a Mach cone (green). The superposition of waves from all points along the rupture front generates a Mach wedge capped at the bottom by half of a Mach cone (light blue). In addition to generating shear Mach waves, a surface breaking rupture also excites Rayleigh Mach waves. Rayleigh waves are surface waves comprised of evanescent shear and dilational waves; they propage at a speed slightly less than the S-wave speed. Consequently, a supershear source is also a super-Rayleigh one, so Rayleigh Mach fronts (dark blue lines) will appear on the free surface slightly behind the shear Mach fronts. These Rayleigh Mach waves were only recently recognized during a recent project together with Harsha Bhat.

Fig. 3: Both analytical and numerical solutions give insight into supershear rupture dynamics. The plot on the left shows the particle velocity field surrounding a slip pulse propagating at a supershear velocity. This was calculated using an analytical solution I derived for a two-dimensional mode II rupture. The shear Mach fronts are clearly visible and the sense of motion (transverse to the Mach front) within the Mach region is consistent with that of radiating shear waves radiating from the fault.

On the right are results from a numerical model of the 2002 Denali Fault earthquake. This magnitude 7.9 event in central Alaska occurred on a strike-slip fault, and is similar in size to what is expected when the San Andreas fault breaks. An accelerometer at Pump Station 10 (PS10), located only 3 km from the fault along the trans-Alaska oil pipeline, recorded the history of ground shaking. The distinctive feature of sub-Rayleigh strike-slip earthquakes is a two-sided fault-normal velocity pulse with little motion in the fault-parallel direction. In contrast to this, the PS10 records show a large one-sided fault-parallel velocity pulse (A) coincident with a slightly smaller one-sided pulse in the fault-normal direction (B). These features are well-fit by a supershear rupture model. Further convincing evidence for supershear propagation comes from a large two-sided fault-normal velocity pulse that arrives a few seconds later (C and D). This two-sided fault-normal pulse is exactly what is expected from slip propagating below the S-wave speed, so one possible explanation of the PS10 record is that rupture took the form of two slip pulses, the first moving at a supershear speed and the second at a subshear speed. While this might sound incredibly unlikely (especially since most kinematic inversions start with the a priori assumption of a single slip pulse), it is actually exactly what elastodynamic considerations predict for a rupture that transitioned from a sub-Rayleigh to supershear speed about 30 km prior to passing PS10. After the transition, the supershear slip pulse propagated along the fault, leaving it in a weakened state. Jumps in rupture speed generate bursts of radiation; some of these waves have phase velocities along the fault that are less than the S-wave speed, so they would trail the supershear slip pulse. A weakened fault acts as a waveguide along which interface waves similar to Rayleigh surface waves can propagate. These interface waves propagate near the Rayleigh speed (exactly at the Rayleigh speed if the fault slides at a constant dynamic friction coefficient) and cause slip on the fault. As part of a project with Ralph Archuleta, I developed a set of spontaneous dynamic rupture models that explored this possibility; one of these models is shown on the right.


homepage
Last updated: November 14, 2007