Zones of seismic shear within major fault zones appear to be highly localized, possibly even to widths in the range of tens to hundreds of microns. Shear within such narrow zones is expected to generate tremendous amounts of heat, sufficient to melt a tabular zone of fault gouge several centimeters wide, unless some physical process reduces shear strength and hence heat production. Together with Jim Rice and Hiro Noda, I have been investigating two thermal effects that are likely to be responsible for this weakening; both are expected to be active from the start of slip in nearly all earthquakes. These weakening mechanisms are flash heating of microscopic asperity contacts and thermal pressurization of pore fluids.
Flash Heating: Recent laboratory friction experiments have achieved seismic slip speeds in the m/s range. For a wide variety of rock types, a dramatic reduction in the coefficient of friction begins around weakening speeds of 0.1-0.3 m/s. The functional dependence of friction coefficient on slip velocity is remarkably consistent with theoretical models for the flash heating of microscopic asperity contacts.
When two surfaces are pressed together, they actually make contact at only a small number of asperities that are tens of microns in diameter. Each asperity contact exists only for a short time before it slides out of existence and is replaced by a new contact. Stresses at these asperities are locally much higher than stresses averaged over the entire surface, and sliding at seismic speeds will produce large amounts of frictional heating. If, during the lifetime of an asperity, the temperature rises to values around the melting temperature (or the temperature at which thermally activated defects become highly mobile), then the shear strength of the contact will drop. Mitigating the temperature rise is thermal diffusion. By balancing thermal diffusion with heat production, an estimate of the critical sliding velocity necessary to initiate weakening can be obtained. This value (~10 cm/s) happens to coindice with what is measured in laboratory experiments. As the sliding velocity increases beyond this weakening velocity, the average shear strength of the population of asperities rapidly drops.
The extreme velocity-dependent weakening associated with flash heating is known to produce self-healing slip pulses if the background stress level on faults is below a critical value. Using parameter values based on laboratory experiments, this critical stress level translates to ratios of shear to effective normal stress around 0.2-0.3. This stress level is far less than would be expected based on standard estimates of friction coefficients around 0.6-0.8, yet is consistent with geodynamic models for the long-term average stress supported along major faults.
Thermal Pressurization: Fault gouge, being porous, is presumably fluid-saturated below the water table. Consequently, increases in pore fluid pressure can relieve the effective normal stress acting on the fault, making it easy to slide. One mechanism for dynamically increasing pore pressure during earthquakes is thermal pressurization. As deformation occurs within narrow shear zones, frictional heating increases the temperature of the rock matrix and pore fluids. While the rock matrix and fluids are equally compressible, thermal expansion coefficient of the fluid is vastly higher than that of the rock. When heated, the fluid tries to expand but, being confined within the rock matrix, instead pressurizes. Diffusion of heat and fluid act to mitigate this pressurization.
While the general theoretical foundation for thermal pressurization was well established over the past several decades (the governing equations are conservation of energy and fluid mass), it is only with recent laboratory measurements of hydraulic properties of ultracataclastic fault-core materials and geologic constraints on the width of shear zones that the importance of the process can be properly assessed.
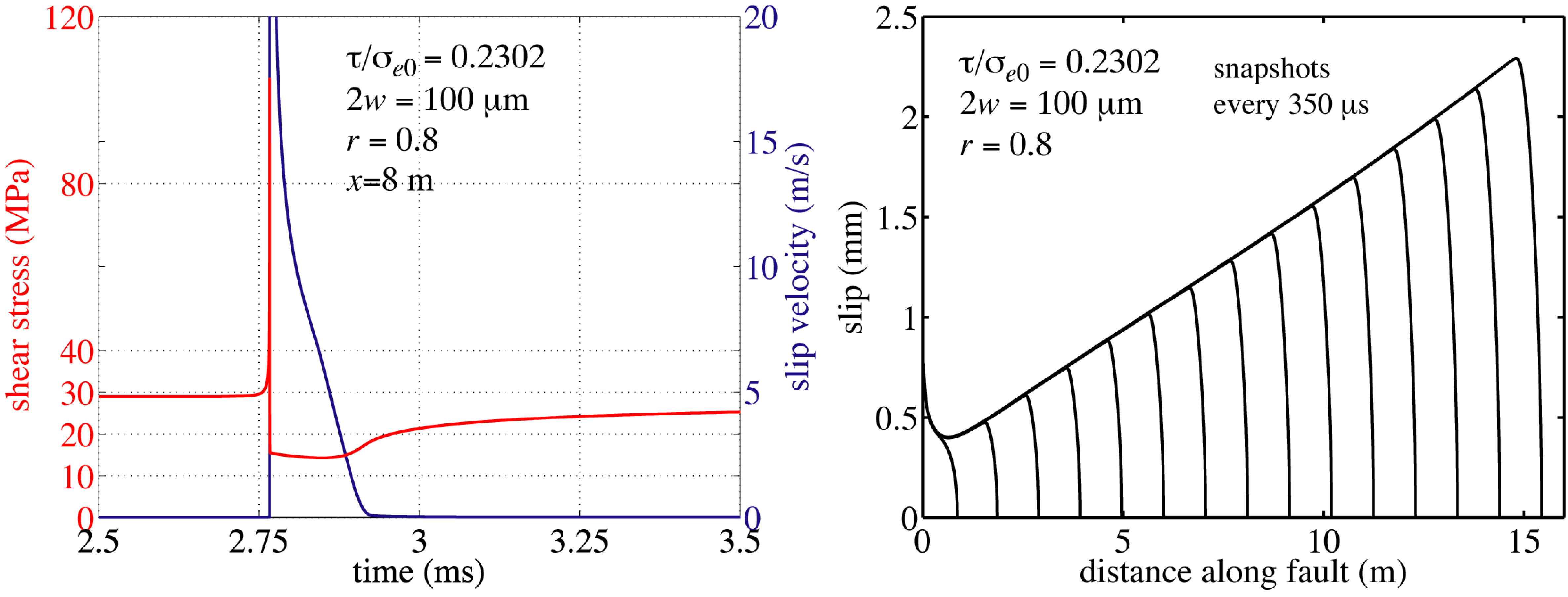
Numerical Simulations: Over the past two years, we have developed numerical methods for incorporating flash heating and thermal pressurization into our spectral boundary integral equation code. At each point on the fault, we defined a finite-difference diffusion grid extending normal to the fault and solved the thermal pressurization equations on it. The time step required to explicitly integrate the constitutive equations without numerical instability is generally an order of magnitude less than that required to integrate the elastodynamic equation. To avoid the additional expense of solving the elastodynamic system at the smaller time step, we developed a substepping procedure wherein we integrate the constitutive equations over many smaller time steps within a single elastodynamic time step. The substep size is chosen adaptively to bound error less than a specified tolerance, making our method extremely robust and efficient for a wide range of parameters. See Fig. 1 for general results from these models.

|
| Fig. 1: (left) Stress and slip velocity history at a point 8 m away from the nucleation zone. Slip initiates when shear stress at the rupture front rises from the low background level to a high static friction value. After slipping at a low stress level, the fault walls relock, and stress increases. The static stress drop is only a few MPa. (right) Slip profile from an expanding slip pulse. Slip increases at a rate of ~0.14 mm/m = 0.14 m/km, consistent with geologic observations. |
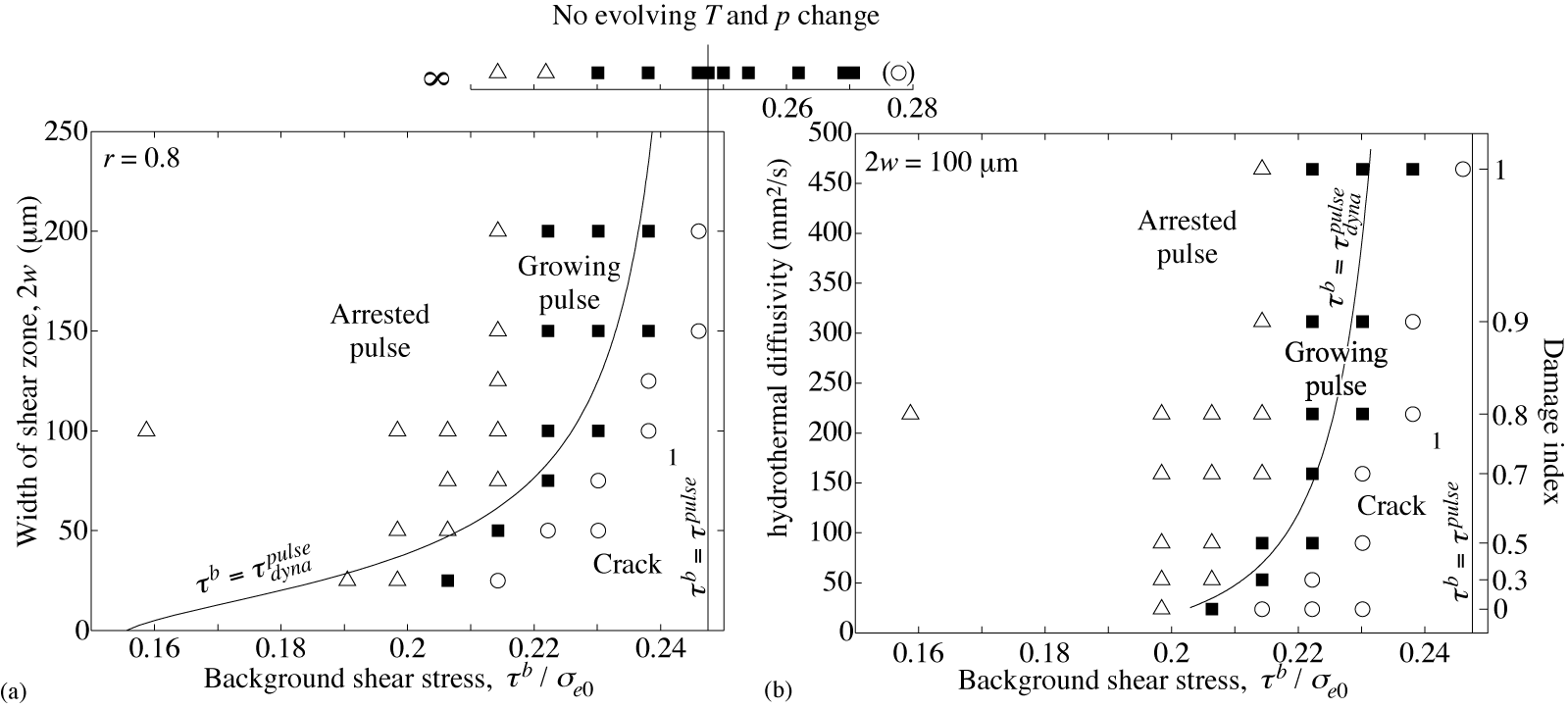
We have numerically explored parameter space with an eye toward producing ruptures consistent with observed phenomenology (e.g., static stress drops of a few MPa, self-healing pulse mode of rupture). While many of the physical properties entering the model are well constrained, others are not. In particular, parameters related to the efficiency of fluid flow through the porous medium (hydraulic diffusivity and the pore pressure change per unit temperature change under undrained conditions) are likely to be altered by inelastic deformation dynamically induced by the stress concentration ahead of the rupture front. Consequently, we explore a range of parameters associated with hydraulic processes (see Fig. 2). An additional uncertainty is the width of the shear zone, which presumably ranges from several tens to hundreds of microns. We have also explored the limiting case in which slip is localized onto a mathematical plane, but find that the finite width of the shear zone, even if less than several hundred microns, can dramatically alter the rupture process (see Fig. 2).
|
| Fig. 2: Phase diagrams for rupture modes (arresting pulse, expanding pulse, and expanding crack) as a function of background shear stress and (a) shear-zone width and (b) hydrothermal diffusivity factor (which reflects the influence of damage on hydraulic parameters). |