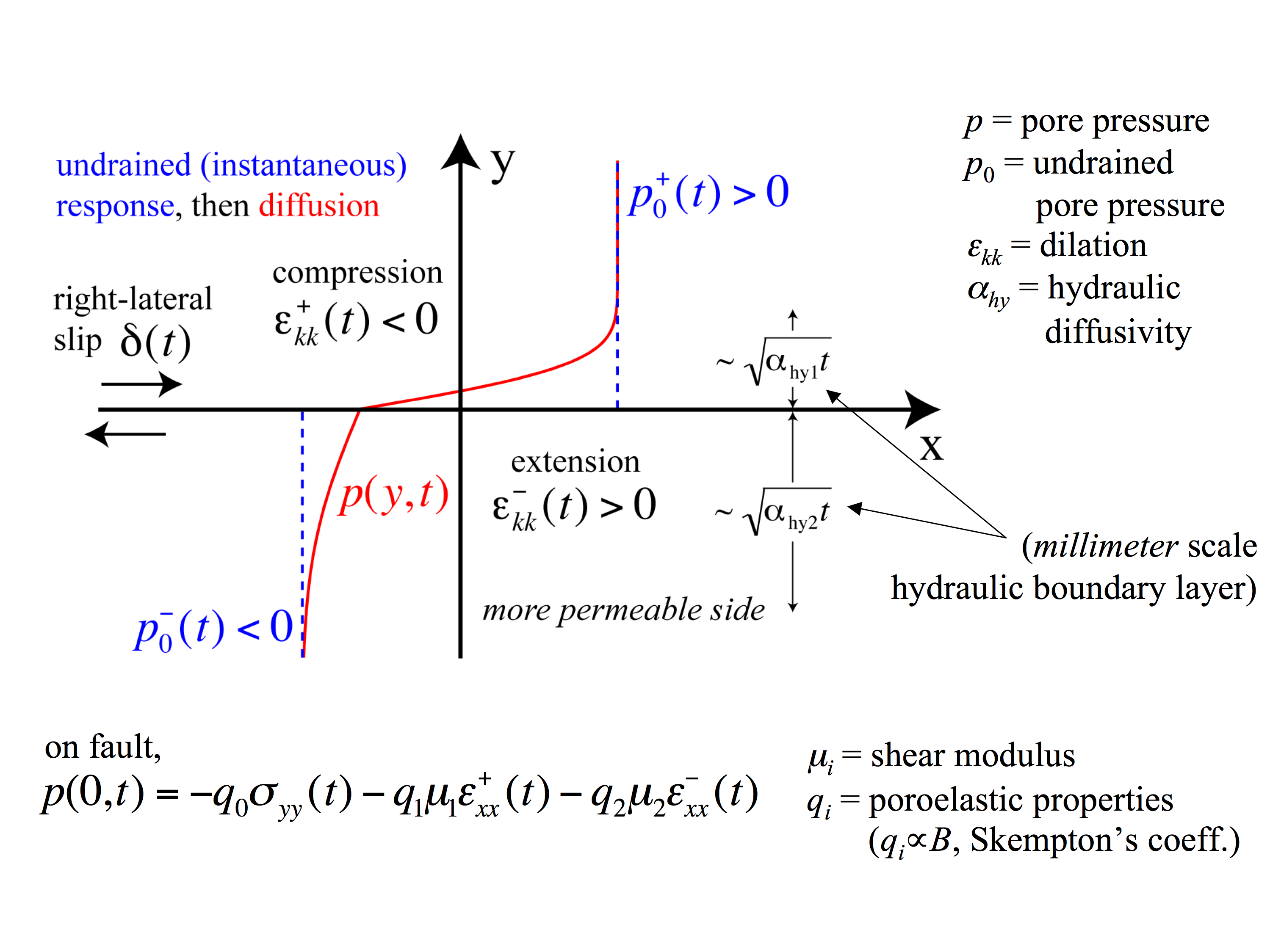
For many applications (e.g., seismic wave propagation) the response of a poroelastic material at the coseismic timescale may be treated identically to that of an elastic material, but using elastic constants corresponding to undrained conditions. This is because fluid flow over the distances of interest is negligible over these short time intervals. A notable exception to this undrained approximation occurs in the immediate vicinity of faults. Since mode II slip compresses one side of the fault and extends the other, the undrained poroelastic response will induce pore pressure changes of opposite sign on the two sides of the fault (Fig. 1). This results in a discontinuity in pore pressure across the fault and, until recently (starting with the work of John Rudnicki and Jim Rice, and continuing in a collaboration between Jim Rice and myself), it was not understood how to evaluate pore pressure on the fault itself. The solution is that diffusion of fluids across the fault, acting to equilibrate this pressure gradient, must be considered to ensure continuity of fluid flux and pore pressure across the fault, thereby removing the discontinuity in pore pressure (Fig. 1). Since fault strength can be reduced by increasing pore pressure, it follows that fault strength is highly sensitive to hydraulic properties within fringes of damaged material on either side of the fault. The relevant distance over which these parameter matter is the hydraulic diffusion length (~mm-cm for fault-zone materials).

|
| Fig. 1: Poroelastic response to volumetric fault-zone strains. Mode II slip compresses one side of the fault and extends the other. The pore fluid pressure instantaneously responds, as shown by the dashed blue lines in the diagram above. This creates a discontinuity in pore pressure across the fault, and fluid flow is driven by this pressure difference. By solving a diffusion equation for each side of the fault, subject to continuity of pore pressure and fluid flux across the fault, one can obtain the actual pore pressure distibution, shown by the red curve. If there is perfect symmetry between the two sides of the fault, then the pore pressure on the fault will remain unaltered. Anything that breaks this symmetry (different magnitudes of compression/extension in the two fault walls, differences in hydraulic properties across the fault, etc.) will induce a pore pressure change on the fault itself. All else being equal, pore pressure on the fault moves toward the undrained response of the more permeable side. The sign of the pore pressure change reverses for ruptures that propagate in the opposite direction since this switches which side is compressed and which is extended. |
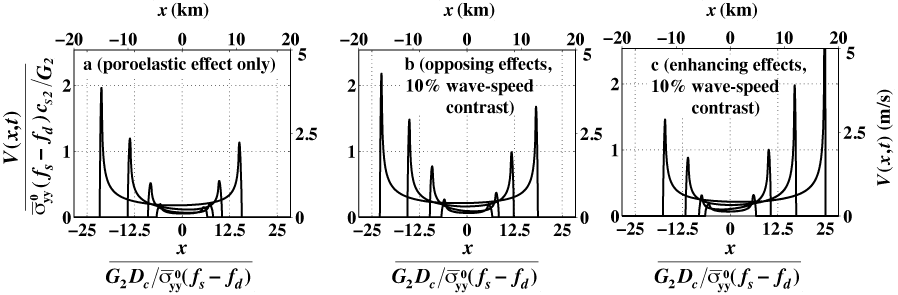
We have considered the case of hydraulic properties that are discontinuous across the fault (as will occur if slip localizes at the boundary between the fault core and surrounding damage zone), but treated these properties as constants, despite the recognition that the stress concentration at the rupture front likely alters the hydraulic response of fault-zone materials. We further neglected "plastic" straining, including inelastic dilatancy. (These are currently active research areas for us.) Despite these simplifications, our work revealed the importance of considering poroelastic effects in rupture dynamics and established how to properly evaluate pore pressure on a fault between poroelastic solids. Fig. 2 illustrates how a contrast in poroelastic properties across the fault can induces induce bimaterial effects that, in many cases, are as large as or larger than those from a mismatch of large-scale elastic properties across the fault.
|
| Fig. 2: Examples of spontaneous rupture simulations between dissimilar poroelastic materials. Shown are snapshots of slip velocity illustrating how changes in effective normal stress (an increase in one propagation direction and a decrease in the other) lead to much higher slip rates in the direction in which effective normal stress is reduced. Case (a) shows rupture between identical elastic materials, but with a factor-of-ten contrast in permeability across the fault. The same degree of poroelastic mismatch is present in cases (b) and (c), but now there is a 10% contrast in wave speeds across the fault. Depending on whether or not the more permeable side is also the side with faster wave speeds, the two effects can either oppose (b) or enhance (c) each other. |